Shack-Hartmann Image Motion Monitor
(SHIMM)

Optical Turbulence

Optical turbulence occurs when layers of air of different temperature mix, resulting in the aberration of starlight propagating through the atmosphere. The atmospheric turbulence induces speckling and movement of the image, called seeing, as well as intensity fluctuations, called scintillation. Image quality and signal-to-noise of astronomical images and photometric measurements depends on the prevailing seeing and scintillation conditions during an observation. The long-term statistics of the seeing are critical for the optimal selection of observing sites. It is important to emphasise that the altitude of turbulent layers, as well as their strength, affect observations in different ways. Seeing (i.e. image distortion) results from all turbulent layers in the atmosphere. Scintillation however, predominately results from high altitude turbulence. Therefore, for example, it is possible to have overall bad seeing but low scintillation noise. For this reason, facility turbulence monitors play an important role for astronomical observations, with regards to site characterisation and the optimisation and queue-scheduling of observations.

SHIMM Instrument

SHIMM instrument
Figure 1: SHIMM on the roof of the INT in La Palma.

One of the most commonly used seeing monitors is the Differential Image Motion Monitor (DIMM) (Sarazin+89). The DIMM is a compact instrument, utilising a small telescope, which measures the differential motion for images of the target star produced by two subapertures within the telescope pupil. The SHIMM, imaged in figure 1, is a variation on the DIMM design, made by employing a Shack-Hartmann Wavefront Sensor (SHWFS) instead of an aperture mask (Perera+16). By using a SHWFS more subapertures can be used as shown in figure 2.

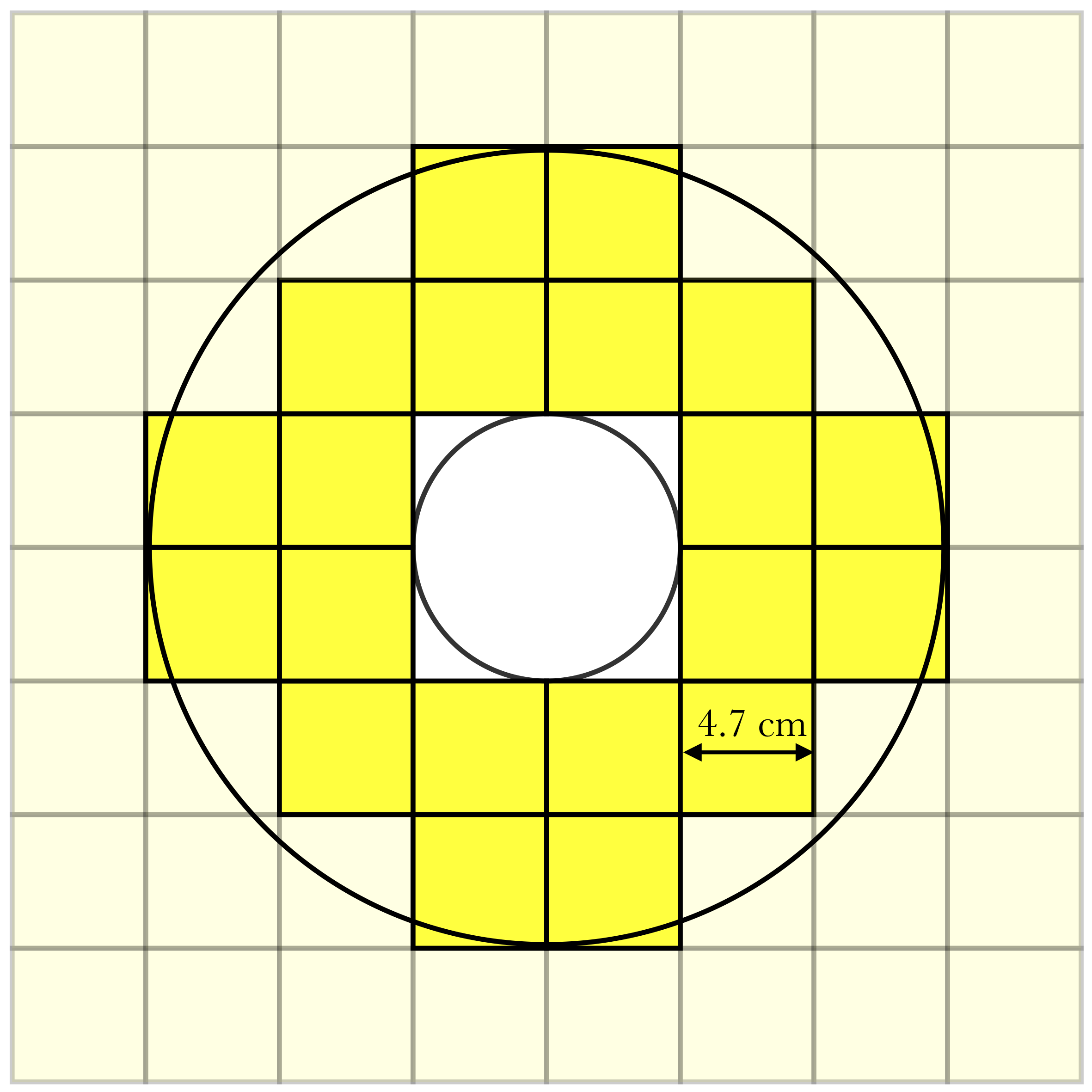
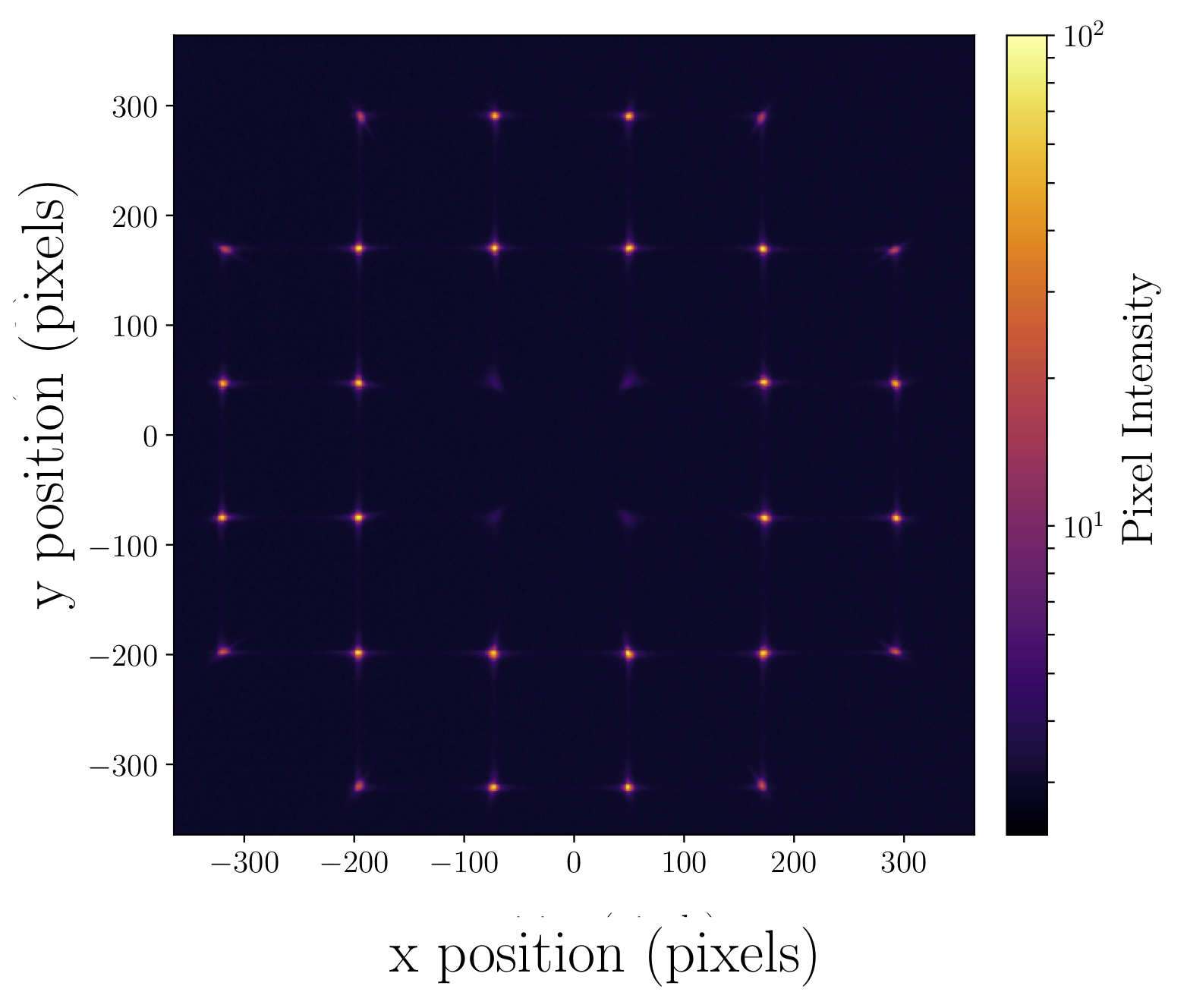
Figure 1: (left) Illustrates the illuminated square subapertures of the WFS mapped onto an 11" telescope aperture. The outer and inner circle indicates the primary and secondary mirror. (right) Shows the resulting spot pattern formed on the CCD. A log scale has been used to present the image, in order to highlight the contrast between the background and the spot pattern.

The SHIMM was developed to serve as a low-cost, compact, portable seeing monitor, that could be easily and inexpensively duplicated, making it ideal for comparisons of atmospheric conditions around a large observing site. The key advantages of the SHIMM over the DIMM is that it can (1) measuring the Fried parameter (r0) independent of noise, (2) measure the coherence time (τ0) and (3) estimate a low-resolution vertical profile of the turbulence.



References